berapa banyak jumlah segitiga pada gambar berikut?

Berapa banyak segitiga (semua ukuran) yang Anda lihat dalam segitiga sama sisi di bawah ini?

Banyak orang mencoba solusi, dan beberapa sudah benar, tapi teka-teki ini membuktikan sedikit lebih menantang daripada menghitung kotak pada papan catur sehingga saatnya untuk memberikan solusi lengkap. Ini mungkin tampak seperti tugas sederhana menghitung segitiga, tapi lebih sulit untuk melacak yang segitiga Anda sudah dihitung daripada dengan kotak. Selain itu, aku selalu lebih tertarik pada pendekatan umum untuk sebuah teka-teki dari saya dalam larutan untuk contoh spesifik dari teka-teki.
Sebelum kita mulai, mari kita sedikit keluar terminologi jalan. Aku akan mengacu pada setiap contoh spesifik dari permasalahan ini dengan jumlah unit-segitiga pada dasarnya. Unit-segitiga adalah segitiga terkecil dalam setiap gambar, dan basis adalah jumlah unit-segitiga sepanjang tepi bawah. Pada gambar di atas, ada lima unit-segitiga di dasar. Mari kita sebut jumlah unit-segitiga di gambar u (n), dimana n adalah jumlah unit-segitiga di dasar, dan jumlah total segitiga di gambar T (n).

Dimulai di awal, kita melihat bahwa kasus yang paling sederhana hanya terdiri dari satu segitiga.


u (1) = 1
T (1) = 1

Selanjutnya kita memiliki segitiga yang memiliki dua segitiga pada dasarnya. Menghitung unit-segitiga kita mendapatkan empat, ditambah segitiga lebih besar yang mereka bentuk, untuk total lima.


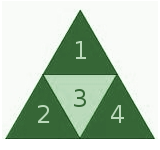
u (2) = 4
T (2) = 5

Selanjutnya kita naik ke segitiga dasar-3. Anda dapat melihat dari gambar di bawah ini bahwa itu terdiri dari 9 unit.


u (3) = 9

Selain itu, ada tiga basis-2 segitiga (satu di setiap sudut, lihat gambar di bawah), ditambah segitiga dasar-3 itu sendiri, untuk total 13.



T (3) = 13

Pada titik ini Anda harus mencatat bahwa setiap segitiga base-n terdiri dari tiga dasar-(n-1) segitiga, satu untuk setiap sudut. Satu-satunya pengecualian pada aturan ini adalah di dasar-2, yang kita lihat terdiri dari empat basa-1 segitiga, satu untuk masing-masing sudut dan satu di tengah. Dari sini, saya tidak akan menggambarkan sudut tiga dasar-(n-1) segitiga.

Sebuah segitiga dengan dasar empat unit terdiri dari dirinya sendiri, 16 unit, tujuh basis-2 segitiga, dan tiga dasar-3 segitiga di setiap sudut, untuk total 27.

u (4) = 16
T (4) = 27

Saya tidak akan menggambarkan semua tujuh dari basis-2 segitiga, tapi banyak orang salah hitung mereka, jadi saya akan daftar mereka dengan nomor unit mereka untuk membantu Anda memvisualisasikan mereka.
{1, 2, 3, 4}
{2, 5, 6, 7}
{4, 7, 8, 9}
{5, 10, 11, 12}
{7, 12, 13, 14}
{9, 14, 15, 16}
{6, 7, 8, 13}

Perhatikan bahwa segitiga terakhir terdaftar, {6, 7, 8, 13}, adalah segitiga ke bawah menunjuk. Hal ini penting karena ada lebih dari yang Anda meningkatkan ukuran dasar, dan karena banyak orang mengabaikan mereka saat menghitung. Pastikan bahwa Anda dapat melihat semua segitiga yang terdaftar sebelum melanjutkan.

Akhirnya, kita sampai pada segitiga dasar-5 yang kita ditetapkan untuk memecahkan di awal. Ini terdiri dari 25 unit, 13 basis-2 segitiga, enam dasar-3 segitiga, tiga basis-4 segitiga di sudut, dan dirinya sendiri dengan total 48 segitiga.

u (5) = 25
T (5) = 48

Aku tidak akan melewati dan menggambarkan ke-48 dari mereka, tapi mudah-mudahan isyarat visual saya disediakan dalam ilustrasi sebelumnya membantu Anda untuk tiba pada hitungan yang sama yang saya lakukan.

Rumus yang diberikan untuk urutan adalah:

T (n) = lantai (n * (n + 2) * (2n + 1) / 8)

Aku bisa berhenti di sana, tapi saya ingin menjelaskan apa fungsi lantai, dan mengapa hal itu diperlukan dalam kasus ini. Fungsi lantai dalam matematika hanya memberi integer terbesar kurang dari atau sama dengan input. Ini hanya putaran ke seluruh nomor terdekat (kecuali input sudah merupakan jumlah keseluruhan, dalam hal output adalah persis seluruh nomor yang sama sebagai masukan).

Untuk melihat mengapa kita perlu lantai hasil perhitungan ini, mempertimbangkan dua hal. Pertama, ketika kita menghitung segitiga di gambar asli, saya harap itu jelas bahwa kita akan selalu datang dengan seluruh jumlah segitiga. Artinya, kita tidak akan pernah memiliki beberapa bagian pecahan dari segitiga tersisa. Jawabannya akan selalu menjadi nilai integer. Kedua, jika kita melihat hasil dari rumus tanpa menggunakan fungsi lantai, kita dapat melihat bahwa hal itu diperlukan.

f (n) = n * (n + 2) * (2n + 1) / 8
f (1) = 1 * (1 + 2) * (2 * 1 + 1) / 8 = 1,125
f (2) = 2 * (2 + 2) * (2 * 2 + 1) / 8 = 5,000
f (3) = 3 * (3 + 2) * (2 * 3 + 1) / 8 = 13,125
f (4) = 4 * (4 + 2) * (2 * 4 + 1) / 8 = 27,000
f (5) = 5 * (5 + 2) * (2 * 5 + 1) / 8 = 48,125

Perhatikan bahwa jika n adalah ganjil, selalu ada suatu sisa pecahan yang tersisa dari menerapkan rumus. Lantai hasilnya menghilangkan residu ini, memberikan kita jawaban yang secara keseluruhan jumlah yang sama kita akan tiba di dengan menghitung.

Karena sisanya selalu persis sama dengan 1 / 8, kita bisa mendapatkan hasil yang sama dengan menggunakan dua rumus yang berbeda, satu untuk input genap, dan satu untuk input aneh. Ini adalah pendekatan yang diambil dengan rumus yang diberikan pada pada artikel Wolfram MathWorld ubin Segitiga.